I’m in my first semester as a Teaching Assistant for Calculus I at NYU. A student recently pointed out to me that my classes are primarily made up of freshmen, so most of my students took their high school algebra courses on Zoom during the pandemic. This seemingly obvious statement led to a huge revelation for me. Many of my students are learning Calculus content just fine, but they don’t know how to factor. On an even more concerning note, many of them seem more averse to math than I remember my peers being just a few years ago.

In the fall of 2022, I took a class at Tulane called Education in a Diverse Society with a fantastic professor named Dr. Brooke Grant. We learned about the relationships between race, gender, sexuality, socio-economic status, and disability status with education, with a focus on K-12 education in New Orleans. Ever since hearing my student’s comment about how the pandemic affected foundational algebra knowledge for a whole high school class, I’ve been spending a lot of time thinking about what I learned from Dr. Grant. She often talked about how the violence and natural disasters in New Orleans have created generational trauma that impedes students’ learning (not to mention their quality of life). The trauma caused by the pandemic, especially among those who were in high school at its peak, has not gone unnoticed . I’ve become increasingly sensitive to the fact that my students experienced a shared trauma at a crucial time for their development- including their mathematical development.

I wrote a short paper for Dr. Grant’s class that examined some of the flaws in mathematics education in the United States. It was one of those papers where instead of struggling to meet the word count, I was struggling to cut it down to within the word limit. I think about it often these days when I get questions about basic algebra in my office hours for Calculus. Before the pandemic, U.S. schools were already failing to provide students with equitable and accessible mathematics education. Now, teachers are met with even greater challenges: we’re working within a broken system to try to make up for the lost years of math knowledge. ‘‘Math trauma’’ is a real thing- students who have begun to associate mathematics with failure often can’t break the cycle. After so many students suffered a gap in their mathematics education, there’s no time like the present to deconstruct the flaws in the existing systems and discuss possible solutions. That’s why I’ve decided to share my paper from last fall in the hopes of starting a dialogue. Click here to download, or read below.

Improving Mathematics Education

In the course of my three years at Tulane, the majority of my interactions with other students have started with the same small talk: “What’s your name?”, “Where are you from?”, and “What’s your major?”. My answer to the latter, “Math and Computer Science,” usually earns me a response along the lines of, “Wow, you must be so smart!” Part of me is starting to believe them. I am a junior on track to graduate a full year early. I am applying to obtain my M.S. in Mathematics in my fourth year of college. I must be good at math, right?

Personal Background

My elementary school had a Gifted and Talented (“GT”) program. When I was in second grade, my teacher recommended me, as well as my classmate Elise, for aptitude testing. The two of us were pulled out of class one day to spend a few hours in the office taking tests in Math, English, History, and Science. A few weeks later, the school called my mom to tell her that I had been identified as GT in English and History. When I talked to Elise at school the next day, she told me that she was GT in all four subjects. By fourth grade, I had been moved into a class of primarily GT students. I would watch the other kids working together on extra math worksheets that were not assigned to me. I remember wishing that I was as smart as them. Math remained my lowest grade throughout middle and high school. I was an A student who made C’s in math. I worked at it to try to appear more well-rounded, but I considered it my greatest weakness academically. When I was first granted disability accommodations in high school, an administrator suggested that I move down a level to a math class I could “handle.” I obliged.

When I started college as a Psychology major, I decided that I would need a better math background for the type of research I was interested in. I took Calculus II my freshman fall, and much to my surprise, I got an A-. My dad convinced me to register for Calculus III in the spring. That class was the first to make me fall in love with math. I felt like everything I had learned in math classes over the years clicked together into a new understanding of our multidimensional, measurable, mathematical world. When the end of the semester came, I slept through the final exam after staying up late to study, but my professor graciously allowed me to take it as soon as I woke up. He emailed me a week later. I opened it anxiously, assuming it had to do with missing the exam. Instead, he informed me that I had earned the highest final exam score in the class. I changed my major almost immediately.

I still thought it had to be a fluke. The following semester, however, I got the same email from my Linear Algebra professor. Next, Real Analysis. Each success gave me confidence. But even now, it is hard to talk myself into believing that I am more than an imposter in this space. I spend every day coding, writing proofs, doing machine learning labs, researching my math seminar paper, and trying to convince my capstone group to build a robot with me. I spend every day feeling like an English-History kid, a not-Math-or-Science kid, playing pretend.

Purpose

Unfortunately, I am not alone in my experiences. Mathematics education in the U.S. is not conducive to academic self-esteem and success. The U.S. is ranked 37th in the world in student math performance (Schleicher, 2018). Approximately three-fifths of students in K-12 and college classes are failing mathematics (Boaler & Foster). Within this failing system, math education also involves significant disparities between students based on race and gender (Berwick, 2019). The purpose of this paper is to explore what our country is doing wrong in math education; how this affects different student demographics; and what policymakers, school districts, and teachers can do to ensure an equitable and effective math education for their students. I hope to make this research the beginning of my own education about becoming the kind of math teacher who engages students, helps them fall in love with math, and builds their confidence. I have learned firsthand that the impacts of early messaging regarding math competency are difficult to shake.

Gender in Math

My math classes in college have been comprised primarily of male students. Out of the Bachelor’s degrees that were awarded by U.S. universities to U.S. residents in 2018, 58% were awarded to women (NCSES, 2018). In math and statistics, however, women received only 42%. This lack of representation is likely related to socialization that begins even before children start school. Studies have found that parents pass down their attitudes about math to their children of their own gender; “mothers in particular communicate math-gender stereotypes to their daughters,” (Casad et. al., 2015). Girls whose mothers have low confidence in their own math skills have higher rates of ‘math anxiety.’ This problem often snowballs when girls begin school, as their “female teachers’ math anxiety impact[s] early elementary school girls’, but not boys’, math achievement and attitudes.” Both parents and teachers should be careful how they speak about their own math abilities, as this can influence children who view them as role models.

Math anxiety is a common issue for students working on timed assessments. Jo Boaler, a Stanford professor who studies mathematics education reform, explains that under the stress of time constraints, “the working memory becomes blocked and the students cannot as easily recall the math facts they had previously studied,” (Montenegro, 2015). She expands that this is particularly common among “higher-achieving students and female students.” In addition to modeling confidence in math skills, this suggests that timed assessments are not a fair metric of students’ abilities due to the biases they create.

Race and De-Tracking

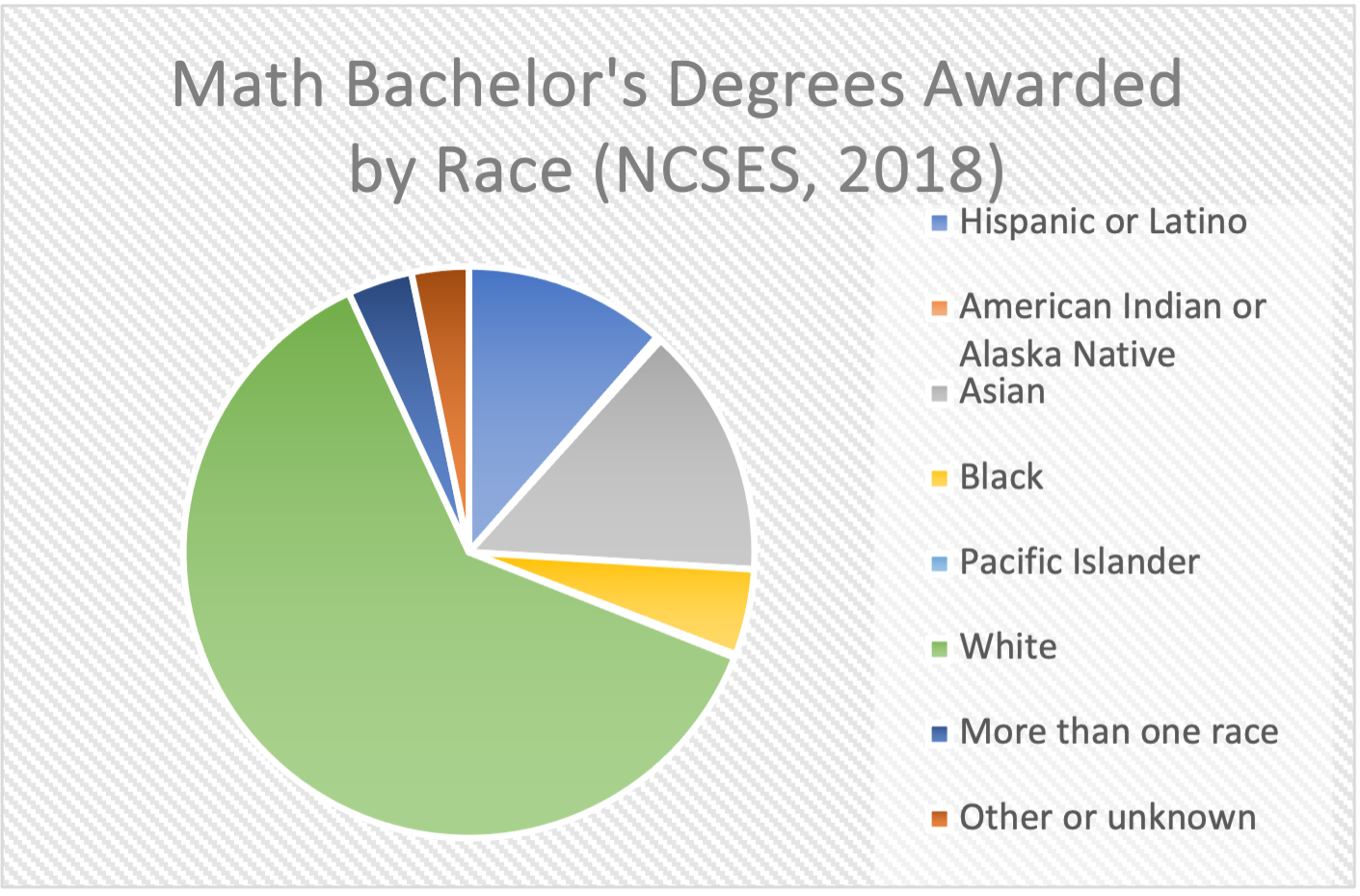
The racial makeup of college mathematics programs is over 60% White (NCSES, 2018). Many researchers have criticized tracking math classes as a contributor to this representation issue. Tracking means grouping students between classes based on their ability. This is a common practice, as 75% of eighth graders are placed in math classes based on ability (Berwick, 2019). Placement in higher-level classes is often biased towards White and Asian students. A 2008-2010 study on San Francisco schools found that “nearly 80 percent of Black and Latino students were placed in General Math, while 55 percent of Asian and White eighth graders were placed in Algebra I, a higher level course.” Over 50 percent of the Black and Latino students in Algebra I had to repeat the class. In 2014, San Francisco eliminated eighth-grade math tracking. All students took General Math in eighth grade and Algebra I in ninth. After this change, the Algebra I repeat rate dropped from 40 percent to 10 percent. “For Black students, the repeat rate dropped from 52 percent to 19 percent, and for Latino students, from 57 down to 14 percent.” The change also resulted in more Black and Latino students taking advanced high school math classes.

Students of all ability levels in higher or lower tracked classes “do not benefit from between-class grouping,” (Steenbergen-Hu et. al., 2016). Students achieve at higher levels when they are “taught in heterogeneous groups, with accompanying good teaching practices,” (Boaler & Foster). Tracking harms students in lower classes by giving them the message that they are not capable of succeeding in challenging math courses. Higher classes often move too quickly to provide students with enough depth of understanding. Our schools should “neither slow down children already experiencing great success, nor put young children on a path to mathematical nowhere,” (Boaler, 2022). Tracked class curricula often ignore the fact that students within each class still have a range of ability levels. De-tracking encourages teachers to provide problems that allow students to demonstrate varying levels of understanding (Boaler & Foster).

Teaching Strategies

Jo Boaler (2022) helped create a framework for California schools to help children fall in love with math by “teaching fewer isolated topics and more connected ideas, with students investigating, problem solving and reasoning, through tasks that engage them deeply.” Reforms that have been implemented across the country “ask teachers to forgo presenting mathematics as a set of facts and procedures and instead help students to make sense of mathematics conceptually,” (Hill, 2021). These reforms have been implemented through standards-aligned textbooks and professional development for teachers. Districts that have implemented reforms have seen “modest” increases in educational quality and “small improvements in teachers’ mathematical knowledge.” Some reformers attribute the slow rate of progress to teachers being “more amenable to incremental rather than wholesale changes in practice.”

Others argue that reformers have gone too far in their focus on conceptual understanding. Rick Hess (2021), an education author and scholar, criticizes reformers’ “disdain [for] memorization in favor of cultivating ‘deeper understanding.’” He argues that “understanding, critical thinking, and problem solving come when students can draw on a strong foundation of relevant domain content, which is built through the ‘rote memorization’ of procedure.” For example, many areas of calculus require students to be able to find trigonometric functions of angles. I was taught how to do this in two different ways at two different schools. In one class, we were taught the “unit circle,” a way to derive the trig functions with reference angles 0,π/6,π/4,π/3, and π/2 using the Pythagorean Theorem. This derivation provided a conceptual understanding of trigonometry, but it was impractical to use as a memorization tool. The unit circle gave my classmates an insufficient foundation to calculate trig values quickly once we had moved on to complex calculus problems. I felt fortunate that I had already taken a class where we were given a chart of the reference angles and their trig values. It was easy to memorize due to its clear pattern and brevity, and we were drilled on using it to compute various angles in our heads. Both classes provided me with very important skills, but I also believe that both teachers failed to provide students with the full set of tools that we needed. Neither memorization nor conceptual understanding alone can prepare students to be successful in math.

Hess (2021) also criticizes reformers for providing open-ended questions without first teaching students how to approach them. He claims that “students need to be given explicit instruction on solving various types of problems, via worked examples and initial practice problems. After that, they should be given problems that vary in difficulty, forcing students to stretch beyond the examples.” This allows students to build their repertoire of mathematical tools by learning the most efficient and practical approaches to different types of problems. Many topics in math involve specific algorithms that always yield a correct answer. Teaching both the algorithm and its conceptual framework are important for building students’ problem-solving ability. Understanding the logic behind an algorithm helps students to retain it, while using the algorithm helps to build conceptual understanding.

Conclusions

Improving mathematics education is a goal that requires educators to rethink the structure of math curricula. Some aspects of the traditional rote memorization approach are helpful in classrooms because they provide students with a foundation they can use to approach problems. Coupled with this, however, is a need for relaying conceptual knowledge that connects topics together, helping students to see the big picture of why each topic matters. Problems provided in classrooms should be structured enough that students can reasonably be expected to apply the tools they have been taught, but open-ended enough that students of different ability levels can demonstrate their levels of understanding within the same classroom. Avoiding strict time limits can also help students to achieve at the level of their ability by alleviating math anxiety.

The tracked structure of many math programs does not benefit students in either the higher or lower level classes. Tracking is discouraging to students in lower classes, and forces students in higher classes to move too quickly to gain a deep understanding of the material. Students of color especially benefit from de-tracked math programs.

De-tracking and reformed classroom practices increase the equitability and success of K-12 math programs. The U.S. is failing to provide students with the mathematical skills that are becoming increasingly important in the global economy. Our children, especially women and students of color, are being refused the opportunity to fall in love with math. This is unacceptable, and we must encourage our governments, school boards, and educators to adopt new policies. If we can help today’s students feel confident and successful in the field of mathematics, they will grow into parents and teachers who model this confidence for future generations.

References

Berwick, C. (2019). Is It Time to Detrack Math? Edutopia. Retrieved October 17, 2022, from https://www.edutopia.org/article/it-time-detrack-math .

Boaler, J. (2022). Op-Ed: How can we make more students fall in love with math? Los Angeles Times. Retrieved October 15, 2022, from https://www.latimes.com/opinion/story/2022-03-14/math-framework-california-low-achieving .

Boaler, J. and Foster, D. (Working paper). Raising Expectations and Achievement: The Impact of Wide Scale Mathematics Reform Giving All Students Access to High Quality Mathematics. Retrieved October 15, 2022, from https://bhi61nm2cr3mkdgk1dtaov18-wpengine.netdna-ssl.com/wp-content/uploads/2017/03/Raising-Expectations.pdf .

Casad, B., Hale, P., and Wachs, F. (2015). Parent-child math anxiety and math-gender stereotypes predict adolescents’ math education outcomes. Frontiers in Psychology. Retrieved October 18, 2022, from https://www.frontiersin.org/articles/10.3389/fpsyg.2015.01597/full .

Hess, R. (2021). What It Takes to Actually Improve Math Education. EducationWeek. Retrieved October 18, 2022, from https://www.edweek.org/teaching-learning/opinion-what-it-takes-to-actually-improve-math-education/2021/06 .

Hill, H. (2021). After 30 years of reforms to improve math instruction, reasons for hope and dismay. Brookings. Retrieved October 17, 2022, from https://www.brookings.edu/blog/brown-center-chalkboard/2021/02/04/after-30-years-of-reforms-to-improve-math-instruction-reasons-for-hope-and-dismay/ .

Montenegro, R. (2015). Stanford Professor: We Need to Take the Fear out of Learning Math. Big Think. Retrieved October 16, 2022, from https://bigthink.com/personal-growth/stanford-professor-we-need-to-take-the-fear-out-of-learning-math/ .

NCSES (2018). Women, Minorities, and Persons with Disabilities in Science and Engineering. NSF. Retrieved October 16, 2022, from https://ncses.nsf.gov/pubs/nsf21321/data-tables .

Schleicher, A. (2018). PISA 2018 Insights and Interpretations. OECD. Retrieved October 18, 2022, from https://www.oecd.org/pisa/PISA%202018%20Insights%20and%20Interpretations%20FINAL%20PDF.pdf .

Steenbergen-Hu, S., Makel, M., and Olszewski-Kubilius, P. (2016). What One Hundred Years of Research Says About the Effects of Ability Grouping and Acceleration on K-12 Students’ Academic Achievement: Findings of Two Second-Order Meta-Analyses. Sage. Retrieved October 17, 2022, from https://journals.sagepub.com/doi/abs/10.3102/0034654316675417 .